C’est un article important, ai-je écrit fin 2021 sur le blog Wasabi Wallet. Je garde ceci ici au cas où le blog serait hors ligne à l’avenir.

J’ai 7 Poufsouffle sur mon compte et vous avez 3 Poufsouffle sur votre compte. Ensuite, je vous envoie 1 Poufsouffle.

Vous connaissez déjà le modèle de compte, c’est ainsi que fonctionne le système bancaire, c’est ainsi que fonctionne Ethereum, mais ce n’est pas ainsi que fonctionne Bitcoin. Bitcoin utilise à la place le modèle UTXO. Pourquoi? C’est un sujet intéressant, mais il n’est pas pertinent pour cet article, alors prenez-le tel quel.

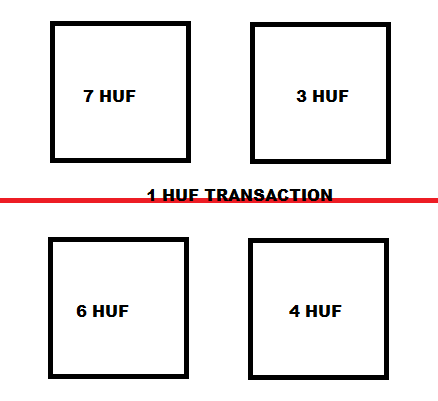
J’ai 7 bitcoins dans mon portefeuille et vous avez 3 bitcoins dans votre portefeuille. Ensuite, je vous envoie 1 BTC.

J’ai construit une transaction qui a une entrée : 7 BTC, et deux sorties : 1 BTC, qui est le vôtre et 6 BTC, ce qui est un changement qui me revient.
Vous disposez désormais de deux pièces : 3 BTC et 1 BTC. Appelons ces pièces Sorties de transaction – TXO. En fait, ces pièces ne sont pas dépensées, nous pouvons donc être plus précis et les appeler sorties de transaction non dépensées : UTXO.

Les Coinjoins sont des transactions Bitcoin collaboratives. Plusieurs personnes participent avec des entrées à une transaction et c’est ce que nous appelons une coinjoin. Faisons-en un !

Mais il y a un problème. Il est trivial de connaître les sous-transactions en corrélant les montants :

6 -> 6
3,1 -> 4

Les Chaumian Coinjoins, spécifiés et mis en œuvre par l’auteur de cet article, se défendent contre la corrélation des montants en se mettant d’accord au préalable sur une dénomination commune : 3 BTC.

De cette façon, personne ne peut dire d’où viennent les 3 BTC UTXO. Bien que nous ayons désormais de l’intimité, ce n’est toujours pas parfait. Cela souffre de trois problèmes principaux.

Création de changement : Avec les corrélations de montants, les observateurs passifs peuvent dire que la sortie de changement de 1 BTC provient de l’entrée de 1 BTC.
Efficacité des espaces de blocs : Les algorithmes Chaumian Coinjoin créent de nombreux résultats.
Structure de transaction limitée : En raison des limitations de conception, l’équipe de coordination de Chaumian Coinjoins peut également déterminer que les entrées 3 BTC et 1 BTC appartenaient au même utilisateur.

Pour résoudre le problème de coordination, nous avons mis au point une nouvelle recherche, appelée WabiSabi, qui nous permet de créer tout type de jointure sans fuite de confidentialité. Nous pouvons désormais ajouter autant d’entrées et créer autant de sorties que nous le souhaitons et nous n’avons même pas besoin de nous mettre d’accord sur des dénominations communes. Du moins pas pour des raisons de coordination.

C’est loin d’être anodin. Deux années de recherches cryptographiques sanglantes ont été consacrées à la résolution de ce problème : comment créer des pièces de monnaie sans confiance avec des montants arbitraires ? Au début, je ne pensais même pas que c’était possible, mais les choses se sont succédées et voilà, c’est résolu ! Nous disposons désormais d’une flexibilité totale concernant l’organisation du montant des pièces de monnaie, alors que faisons-nous avec une telle puissance ?

Jusqu’à présent, nous avons travaillé sur des problèmes bien définis. Les mélangeurs centralisés volaient les fonds des utilisateurs et pouvaient les désanonymiser… alors voici les coinjoins à la rescousse. Les Coinjoins sont désanonymisables par des corrélations de montants… alors voici Chaumian Coinjoins à la rescousse. Les Chaumian Coinjoins limitent cryptographiquement la structure des transactions coinjoin… alors voici WabiSabi à la rescousse.

Et maintenant, nous nous retrouvons confrontés à l’insondable complexité du monde réel. D’innombrables variables conduisent à des problèmes mal définis. Il n’existait aucun moyen logique de progresser de bas en haut, c’est pourquoi un changement de stratégie était nécessaire. Nous avons décidé d’appliquer le plus ancien outil dont disposent les humains : l’intuition, pour proposer de nombreux algorithmes intuitifs pour structurer les coinjoins et voir lequel donne les meilleurs résultats.

Les Coinjoins Dynadenomination utilisent non seulement plusieurs dénominations, mais également plusieurs systèmes de dénomination, de manière aléatoire et dynamique. Je m’attends à ce que ce système soit amélioré jusqu’à la sortie de Wasabi 2.0, les idées et les commentaires sont très encouragés ! Je pense que cela contient déjà toutes les techniques que nous allons appliquer, donc c’est suffisamment développé pour en parler. Permettez-moi d’abord de décrire l’algorithme, puis de poursuivre son analyse.

Nous avons créé une simulation de nos coinjoins de dynadenomination de la manière suivante :

Nous avons d’abord pris quelques mois de nouvelles entrées de coinjoin du monde réel Wasabi Wallet. Frais signifie qu’ils n’ont jamais été mélangés auparavant. Ce sont les montants que les utilisateurs mélangent dans le monde réel.
Nous avons continué notre préparation en regroupant aléatoirement ces nouvelles quantités et avons appelé ces groupes d’utilisateurs, puis avons exécuté notre algorithme de mélange.
Ensuite, nous avons refait le même regroupement, mais seulement 70 % des entrées simulées provenaient de nouveaux montants, le reste provenait du résultat de la première simulation de coinjoin. C’est ainsi que les remix étaient simulés. 30 % sont également basés sur les statistiques réelles du remix de Wasabi Wallet.
Finalement, j’ai exécuté le mixage et écrit les résultats.

Nous pouvons voir que dans notre simulation, 100 utilisateurs ont participé avec 300 entrées au total. Certains utilisateurs ont participé avec moins de 3 contributions, d’autres avec plus. Dans le monde réel, nous ne pouvons pas connaître le nombre d’utilisateurs, mais il s’agit d’une simulation, la simulation a créé ces regroupements, donc nous connaissons exactement les liens grâce à cela. Cette coinjoin a donné lieu à 404 sorties, à l’exception de deux sorties, toutes ayant obtenu un ensemble d’anonymat mathématiquement vérifiable. En moyenne, une sortie comporte 5 jeux d’anonymat. Ce serait déjà cool en soi, mais les garanties de confidentialité ne s’arrêtent pas à des calculs naïfs d’anonymat. Mais d’abord, permettez-moi de décrire l’algorithme ci-dessus.

Imaginez que vous êtes un utilisateur. Vous connaissez le groupe de montants d’entrée auxquels vous participez au coinjoin et vous connaissez les montants d’entrée des autres.
Vous créez également une grande liste de dénominations à partir de plusieurs systèmes de dénomination. Dans ce cas, nous travaillons avec des puissances de 2 (1, 2, 4…), puissances de 3 (1, 3, 9…), puissances de 3×2 (2, 6, 18…), puissances de 10 (1, 10, 100…) et les séries de valeurs privilégiées (1, 2, 5, 10, 20, 50…)
Pour terminer la configuration, créons une grande liste de nos dénominations possibles : 1,2,3,4,5,6,8,9,10,16,18,20,27,30,32,…

Afin de décider quels résultats vous souhaitez créer, créez d’abord un tableau de fréquences en décomposant avidement chaque montant d’entrée avec notre système multidénomination. Par exemple, les entrées 28 et 29 serait décomposé en 27, 1 et 27, 2 respectivement. Dans ce cas, notre tableau de fréquence contient les éléments suivants : 1:1 , 2:1 et 27:2 . Convenons que la dénomination du cycle de coinjoin actuel sera celle des dénominations qui se sont produites au moins deux fois dans la répartition. Dans notre exemple, ce serait seulement 27ce qui montre non seulement que l’exemple est trop simple, mais aussi que cet algorithme ne fonctionne pas pour très peu d’entrées, il ne commence à avoir un sens qu’à partir d’une cinquantaine d’entrées.
Enfin, prenez la somme de vos entrées et décomposez-la en dénominations fréquentes sélectionnées, mais cette fois pas de manière avide, mais plutôt de manière quelque peu aléatoire. Par exemple, si nous trouvons des dénominations fréquentes 1, 4, 6 et la somme de nos entrées est 8 puis avec avidité tu le décomposerais en 6, 1, 1. Mais avec un peu d’optimisation, vous pourriez constater que décomposer votre somme en 4, 4 serait mieux, car cela crée moins de sorties et c’est hautement souhaitable, car l’espace de bloc est rare. Cependant, trouver des répartitions optimales est un problème exponentiellement complexe, nous ne pouvons donc utiliser ici que des heuristiques et ces heuristiques doivent être agrémentées d’un certain caractère aléatoire pour des raisons de confidentialité.

Wasabi 2.0 hérite des garanties de sécurité et de confidentialité de Wasabi 1.0, à savoir : personne ne peut voler vos pièces, le coordinateur ne peut pas corréler vos entrées avec vos sorties et la garantie d’anonymat naïf, qui est ce que vous pouvez voir sur la blockchain, avec la vôtre. yeux, vous pouvez compter le nombre de sorties égales que personne ne peut distinguer.

Cependant, Wasabi 2.0 semble affaiblir la garantie de confidentialité définie par l’anonymat en créant des sorties de quantité égale et plus petite. Wasabi 1.0 crée idéalement 100 sorties égales, Wasabi 2.0 en fait beaucoup moins. Au début, cela peut ressembler à un compromis en matière de confidentialité pour éviter la création de changements et l’augmentation des résultats, ce qui était prévu au départ. Mais en y regardant de plus près, nous avons constaté que les garanties de confidentialité sont bien plus importantes, en raison du grand nombre de sous-transactions. Prenez une sortie du groupe de sortie suivant :

Il y a 7 occurrences de sortie de 0,01 BTC.

Vous pensez peut-être que l’ensemble d’anonymat de la sortie choisie est de 7, mais en réalité, ce n’est qu’une estimation minimale. C’est bien plus haut que ça ! Cela pourrait potentiellement provenir de nombreuses entrées différentes, pas seulement de sept d’entre elles.
Pour avoir une idée de cela, prenons la transaction suivante : 1, 1, 2, 4 -> 2, 2, 4
4 n’apparaît qu’une seule fois côté sortie. Son anonymat naïf est défini sur 1. Mais il se pourrait aussi que 1, 1, 2 provenait du même utilisateur. Par conséquent, son ensemble d’anonymat est de 2, car il existe 2 groupes différents d’entrées d’où la sortie aurait pu provenir.
L’algorithme Dynadenomination Coinjoin a commencé par décomposer chaque entrée en dénominations et a pris les plus fréquentes. Cela a non seulement été utile pour obtenir des égalités probabilistes du côté de la sortie, mais ce sont également d’excellents nombres pour augmenter leurs combinaisons, car ils s’additionnent pour obtenir de nombreuses combinaisons d’entrée. En d’autres termes, les résultats finaux finissent par donner lieu à des sous-cartographies (sous-transactions) plus valides que s’ils devaient être choisis au hasard. De plus, je parle ici en exponentielles. Les combinaisons d’entrées et les combinaisons de sorties sont des nombres énormes.

L’analyse complète des coinjoins Wasabi 2.0 est difficile sur le plan informatique et sera probablement impossible pendant des décennies, car une explosion de complexité combinatoire se produit lorsque nous essayons de trouver toutes les sous-transactions d’un coinjoin Wasabi 2.0.

Un algorithme de force brute devrait

Prenez toutes les combinaisons possibles de regroupement des entrées : 2^number of inputs .
Prenez toutes les combinaisons possibles de regroupement des sorties : 2^number of outputs .
Enfin, vérifiez l’égalité de chaque combinaison pour trouver une sous-transaction. Cela prendrait 2^number of inputs * 2^number of outputs itérations.

Dans le cas de notre exemple de transaction : 100 entrées, 300 sorties, ce serait :

Dans un document de recherche de 2017, Anonymous CoinJoin Transactions with Arbitrary Value, les auteurs ont mesuré le temps de traitement qu’il leur a fallu pour trouver tous les mappages valides des transactions coinjoin : pour toujours. Plus tard, mais indépendamment, les gars travaillant sur CashFusion ont observé la même chose.

C’est tout ce que je note ici, car nos cryptographes me botteront le cul si j’essaie de faire des réclamations sur Wasabi en s’appuyant sur la confidentialité informatique. Néanmoins, je considère toujours cela comme un ajout épicé.

Wasabi 2.0 offre une confidentialité décemment vérifiable basée sur des calculs naïfs d’anonymat et une énorme confidentialité probabiliste basée sur l’inflation des sous-transactions. Mais cela est inanalysable en raison de la troisième garantie épicée : la confidentialité informatique, qui est théoriquement peu solide, mais pertinente en pratique.

Share this content: